Общая характеристика симплекс метода

(2.4)

(2.5)

, , (2.6)

Задача (2.4)-(2.6) имеет предпочтительный план. Её начальный опорный план имеет вид

Если некоторые из уравнений (2.2) имеют предпочтительный вид, то в них не следует вводить искусственные переменные.

Теорема.

Если в оптимальном плане

(2.7)

М-задачи (2.4)-(2.6) все искусственные переменные , то план является оптимальным планом исходной задачи (2.1)-(2.3).

Для того чтобы решить задачу с ограничениями, не имеющими предпочтительного вида, вводят искусственный базис и решают расширенную М-задачу, которая имеет начальный опорный план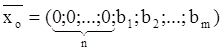

Решение исходной задачи симплексным методом путем введения искусственных переменных называется симплексным методом с искусственным базисом.

Если в результате применения симплексного метода к расширенной задаче получен оптимальный план, в котором все искусственные переменные , то его первые n компоненты дают оптимальный план исходной задачи.

Теорема.

Если в оптимальном плане М-задачи хотя бы одна из искусственных переменных отлична от нуля, то исходная задача не имеет допустимых планов, т. е. ее условия несовместны.

Признаки оптимальности.

Теорема

. Пусть исходная задача решается на максимум. Если для некоторого опорного плана все оценки неотрицательны, то такой план оптимален.

Теорема. Если исходная задача решается на минимум и для некоторого опорного плана все оценки являются неположительными, то такой план оптимален.

Для привидения системы ограничений неравенств к каноническому виду, необходимо в системе ограничений выделить единичный базис.

I. Ограничения вида «0»- ресурсные ограничения. Справа находится то что мы используем на производстве, слева - то что получаем. При таких ограничения вводят дополнительные переменные с коэффициентом «+1», образующие единичный базис. В целевую функцию эти переменные войдут с коэффициентом «0».

II. Ограничения вида «=». Часто бывает, что несмотря на то что ограничения имеют вид равенства, единичный базис не выделяется или трудно выделяется. В этом случае вводятся искусственные переменные для создания единичного базиса - Yi. В систему ограничений они входят с коэффициентом «1». а в целевую функцию с коэффициентом «M», стремящимся к бесконечности (при Fmin - «+M», при Fmax - «-M»).

Экологические заметки

Разработка комплекса мер по оценке воздействия на окружающую среду
Актуальность работы: Ушедшее столетие ознаменовалось резким обострением противоречий в сфере «общество - природа». С одной стороны удовлетворение растущих потребностей населения в ...

Состояние природной среды Смоленской области и ее охрана
Несмотря на спад производства и осуществление ряда мер как на федеральном, так и на региональном уровнях, экологическая обстановка в наиболее населенных и промышленно-развитых рай ...

Региональный комплекс загрязнений окружающей среды (на примере г. Тольятти)
На современном этапе своего развития общество все больше сталкивается с проблемами обеспечения экологической безопасности сформировавшихся эколого-экономических систем и их структу ...